Model-Based Reinforcement Learning: A Survey

This blog is my brief summary about this survery paper. ^[1]

Introduction

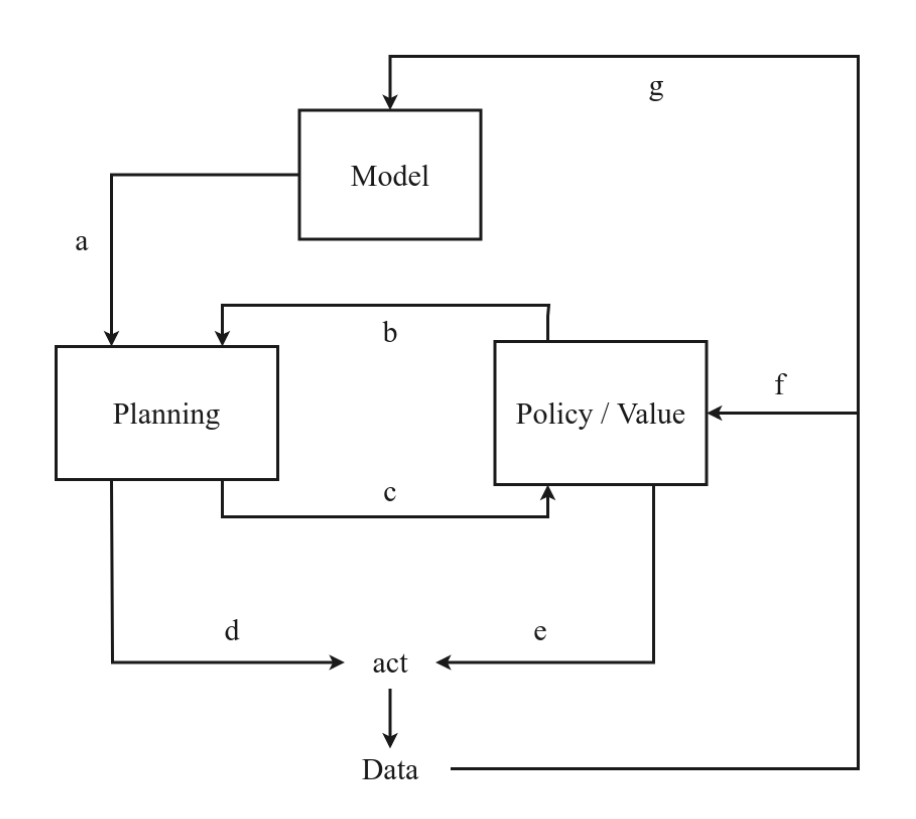
The above figure shows an overview of possible algorithmic connections between planning and learning.

• (a) plan over a learned model
• (b) use information from a policy/value function to improve planning
• (c) use the result from planning to train the policy/value function
• (d) act in the environment based on the planning outcome
• (e) act in the environment based on policy/value function
• (f) train the policy/value function based on experience
• (g) train the model based on experience

Concepts

Reversible access the MDP dynamics is repeatedly planning forward from the same state (Planning methods, humans plan in their mind).

Irreversible access to the MDP means that the agents has to move forward from the resulting next state after executing a particular action. (Model-free methods, human act in the real world)

Model is a form of reverisble access to the MDP dynamics (known or learned)

Local solution only stores the solution for a subset of all states. (Planning method)

Global solution stores the value/policy function for the entire state space. (Learning method)

Planning is a class of MDP algorithms that 1) use a model and 2) store a local solution.

Reinforcement learning is a class of MDP algorithms that store a global solution.

Model-based reinforcement learning is a class of MDP algorithms that 1) use a model, and 2) store a global solution.

Categories of planning-learning integration

• Model-based RL with a learned model, where we both learn a model and learn a global solution. (Dyna)
• Model-based RL with a known model, where we plan over a known model, and only use learning for the global solution. (AlphaZero, Dynamic Programming)
• Planning over a learned model, where we do learn a model, but subsequently locally plan over it, without learning a global solution.

Dynamics Model Learning

Model learning is essentially a supervised learning problem
Dynamics models is to learn the transition probabilities between states.

Type of model

• Forward model: $(s_t,a_t)\rightarrow s_{t+1}$
  Most commeon model can be used for lookahead planning.
• Backward/revers model: $s_{t+1}\rightarrow (s_t,a_t)$
  Plan in the backwards direcion (Prioritized sweeping)
• Inverse model: $(s_t,s_{t+1})\rightarrow a_t$
  Useful in representation learning (RRT planning)

Type of approximation method

• Parametric: The number of parameters is independent of the size of the observed dataset.
  • Exact: For a discrete MDP (or a discretized version of a continuous MDP), a tabular method maintains a separate entry for every possible transition. However, they don not scale to high-dimensional problems (the curse of dimensionlity)
    • Tabular maximum likelihood model
      $$T(s^\prime|s,a) = \frac{n(s,a,s^\prime)}{\sum_{s^\prime} n(s,a,s^\prime)}$$
  • Approximate: Function approximation methods lower the required number of parameters and allow for generalization.
    • Linear Regression
    • Dynamic Bayesian networks (DBN)
    • Nearst Neighbours
    • Random forests
    • Support vector regression
    • Neural Networks
• Non-parametric: Directly store and use the data to represent the model. And the computational complexity of non-parametric methods depends on the size of the dataset. So less applicable to high-dimension problems where normal require more data
  • Exact: Replay buffers
  • Approximate: Gaussian processes

The region of state space

• Global: Approcimate the dynamics over the entire state space. (Main approach)
• Local: Locally approximate the dynamics and discard the local model after planning over it.

Reference:

1. Moerland, T. M., Broekens, J., Plaat, A., & Jonker, C. M. (2022). Model-based Reinforcement Learning: A Survey (No. arXiv:2006.16712). arXiv. doi: 10.48550/arXiv.2006.16712 ↩